Using average active linear regression for BLS estimate
In our last post we attempted to predict the CES total nonfarm, non-seasonally adjusted dataset from BLS using LinkUp’s dataset as our independent variable, and utilizing a linear regression model.

In our last post we attempted to predict the CES total nonfarm, non-seasonally adjusted dataset from BLS using LinkUp’s dataset as our independent variable, and utilizing a linear regression model. Our first attempt at that prediction was directionally correct: BLS reported around 144,005 non-seasonally adjusted jobs, and our prediction was 147,205. Not a bad start, but there is certainly room for improvement.
In the last post, we mentioned there were some ways to improve on our methodology. The first is to focus on eliminating the revisions that BLS bakes into their process. To do this, we will need to find a dataset of non-revised BLS employment numbers. Since our CEO has been making these predictions for years, he has this set handy; and it is what we will be using for the prediction. As we proceed, it’s important to note that this BLS dataset is seasonally revised.
What we notice using this set is that our original LinkUp total active jobs dataset used in the first no longer correlates well with our new BLS set.

Given the lack of correlation, it makes sense to consider a few additional factors. In the previous post, we used preagregated files for our independent variable. Being that those factors no longer relate to this dataset, we transitioned to using the raw job records themselves. The disadvantage is that this takes a bit more effort on our end, but provides us with many advantages in the form of custom calculations and advanced filtering.
One thing we can now control for is the rate of growth of the companies within our sample. Previously, we did not have the capability to do this. BLS controls the rate of growth using a specific formula. That formula seems to roughly average a net addition of around 500 firms a year. We will attempt to mimic this by limiting the sample of companies to only those that LinkUp indexed in 2012, and only allowing half of the companies LinkUp has created going forward to enter into our sample. We can also filter out by specific occupations now, so we will take advantage of this and eliminate some farm specific ONET codes.
Next we will take the raw records and create the usual factors of created, deleted, active, but also add average active (for which will average the daily active count).
Now that we have our features, we can determine if one of these relates to our independent variable.
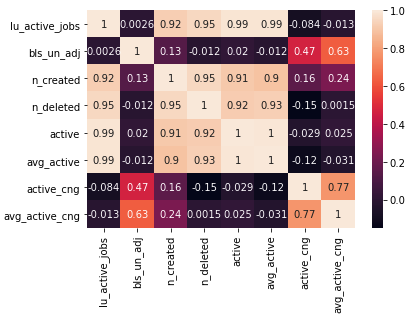
It appears that our newly created average active variable shows moderate correlation to our independent variable. Next, we create a linear model and input our series. With our prediction coming in at -1,362,739.
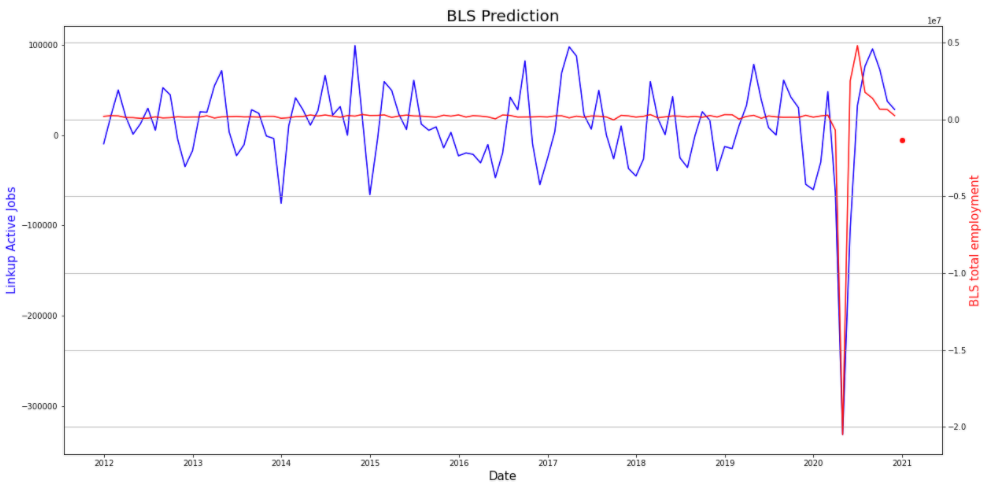
This would be a massive decrease and it tells us that something is likely throwing our model off. A quick glance reveals that we do have some large outliers, but those are recent accurate data points, so we would not remove them. It looks as though LinkUp’s data saw a large decrease in jobs in December. We are also now working with BLS’s seasonally adjusted dataset. Let’s perform a simple seasonal adjustment by subtracting the year’s value from each month and see what our results look like.
With that adjustment we are seeing a large, but slightly more realistic, increase of 417,402 – though that still seems improbable. We can try a more in-depth seasonal adjustment that takes the residual of our series, and creates a seasonal factor to adjust by monthly. By applying this we get a result of -113,745 jobs added. Given the news surrounding the employment situation, this seems like a realistic prediction. We can compare this to the original performance of our first model, keeping in mind it is predicting the non-seasonally adjusted dataset with a prediction for this month of 147,939 total non farm, non seasonally adjusted jobs.
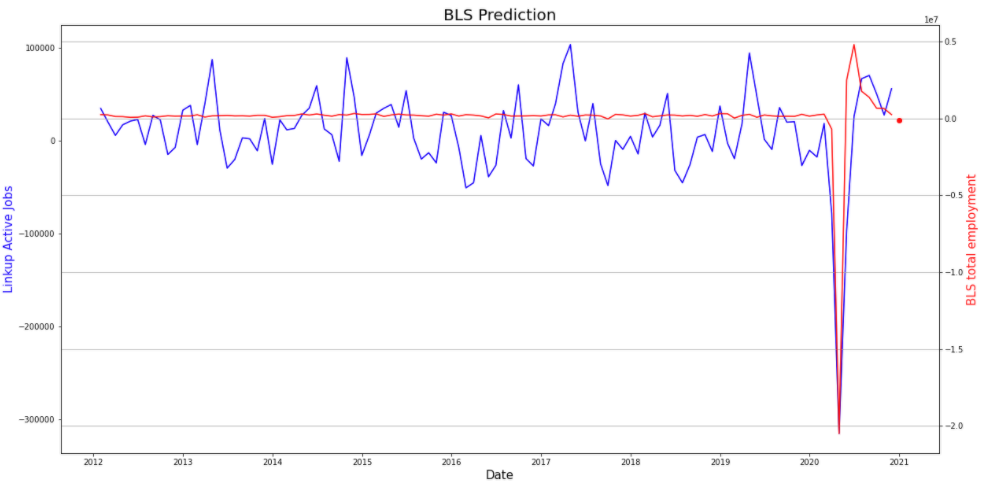
A lot has changed in this iteration, so we will compare our prediction to the original simpler model to see if we are moving in the right direction. That model produced a prediction of 147,939 jobs gained: a smaller gain compared to last time.
Stay tuned for our next tutorial in this series. For more about the data behind this post, please contact us.
Insights: Related insights and resources
-
Blog
06.29.2021
Wage inflation: Overhyped or rising concern?
Read full article -
Blog
03.04.2021
More from our BLS linear regression series
Read full article -
Blog
12.03.2020
Using simple linear regression for BLS estimate
Read full article
Stay Informed: Get monthly job market insights delivered right to your inbox.
Thank you for your message!
The LinkUp team will be in touch shortly.
